Мир звуков! Как он разнообразен и неповторим! Разве можно спутать шум морского прибоя и щебетание птиц, возгласы болельщиков на стадионе и шелест листьев, вой взлетающего реактивного самолета и мяуканье котенка. Так же просто отличить игру симфонического оркестра от игры ансамбля гитаристов. Примеров таких мы могли бы привести множество. Ведь восприятие звуков - это не что иное, как ощущение, воздействующее на слушателя.
Что же такое звук?
Чтобы ответить на этот вопрос, давайте совершим небольшую экскурсию в мир звуков.
Сейчас все знают, что звук есть процесс колебательный. В предыдущей главе мы рассказали о физике Юнге, впервые зафиксировавшем следы звуков. И удалось это ему потому, что он установил: звук - это процесс колебания воздуха. А раз звук - процесс колебательный, то его можно зафиксировать. Сконструированный им для этого прибор полностью подтвердил предположения ученого, а 1807 год стал годом открытия этого явления.
С механическими колебаниями твердых тел вы, очевидно, подробно познакомились в школе. Напомним все же вкратце о колебательном процессе, чтобы помочь вам понять сущность звуковых колебаний.
Классическим представителем колеблющегося тела является маятник. Вспомните опыт, который обычно демонстрируют на уроках физики. Если грузик, подвешенный на нитке, отвести от положения равновесия, то он начнет совершать повторяющиеся движения, каждый раз возвращаясь в исходную точку и дважды проходя через положение равновесия. Следовательно, колебательное движение есть движение повторяющееся или, как говорят, периодическое. А в технике периодические колебания называют еще и гармоническими. Одна из важнейших характеристик такого процесса - это период колебания, или просто период, обозначаемый буквой Т. Период колебания показывает, за какое время колеблющееся тело совершает полный цикл движения. Для маятника периодом колебания будет время, за которое он совершит одно колебательное движение и вернется в исходную точку. Другая важная характеристика периодического колебания - амплитуда колебания, или просто амплитуда. Для маятника это будет расстояние от точки равновесия до исходной точки, или наибольшее отклонение от положения равновесия. А теперь давайте попробуем «развернуть» колебательное движение маятника. Для этого к маятнику прикрепим кусочек грифеля от карандаша и поместим под маятником лист бумаги. Когда бумага неподвижна, грифель на маятнике будет прочерчивать прямую линию. Но стоит начать равномерно передвигать бумагу в направлении, перпендикулярном к плоскости колебания маятника, как грифель прочертит кривую линию, повторяющуюся столько раз, сколько колебаний совершит маятник. Эта кривая линия показана на рисунке. Называется она синусоида.
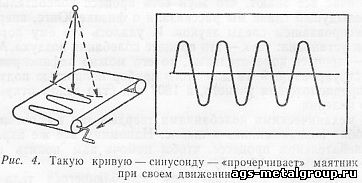
Проделаем еще один опыт с маятником. Отведите грузик, подвешенный на нитке, и дайте ему возможность свободно колебаться. Вы заметите, что эти колебания маятника будут продолжаться довольно долго, а чем тяжелее грузик, тем дольше будет колебаться маятник, причем его колебания в начальном периоде будут иметь неизменную амплитуду. Теперь этот же грузик отвяжите от нитки и прикрепите к дощечке, а в ее противоположном от грузика конце просверлите отверстие. Вставив в это отверстие гвоздь, мы опять получим колебательную систему, но теперь уже несколько измененного вида. Приведя в движение этот маятник, мы убедимся, что он довольно быстро прекращает свои колебания, а их амплитуда постепенно уменьшается. Сравнивая между собой оба колебательных процесса, можно сделать вывод, что существуют два вида колебаний, одно из которых имеет постоянную амплитуду и продолжается довольно долго (можно сказать - бесконечно), а другое имеет постепенно убывающую амплитуду и быстро прекращается. Первое из этих колебаний называется незатухающим, а второе - затухающим.
Говоря о колебаниях маятника, мы ни словом не обмолвились о среде, в которой он совершает свое движение. А ведь среда не может остаться безучастной к любому движению, в том числе и к колебательному, и ее частицы при этом будут, сжимаясь, смещаться из одного положения в другое, близлежащий слой среды будет влиять на более отдаленный слой, тот, в свою очередь, будет влиять на следующий слой и т. д. Движения частиц среды будут подобны движению воды, когда она расходится кругами от брошенного в нее камешка. Такие колебания среды называют звуковыми, хотя не все они могут быть услышаны. В физике понятие «звуковые колебания» используется в более широком смысле.
Звуковые колебания могут возникать в любой среде, способной сжиматься. Изучением таких колебаний занимается наука, называемая акустикой. Но нас интересуют не колебания вообще, а только колебания в воздухе, которые вызывают слуховые ощущения.
Итак, во время звуковых колебаний элементарная частица воздуха, оставаясь на месте, будет совершать колебания около положения равновесия. Как и в случае с маятником, такие колебания характеризуются амплитудой и периодом колебания. Однако в технике обычно пользуются величиной, обратной периоду, которую называют частота. Она показывает количество колебаний в единицу времени. Частота, при которой за 1 секунду происходит один цикл периодического процесса, получила обозначение герц (Гц). Например, переменный ток в электрической сети имеет 50 колебаний в секунду. Но мы обычно говорим, что частота переменного тока в электрической сети 50 герц.
Чтобы иметь полное представление о звуковом колебании, напомним еще об одной физической величине, характеризующей периодические колебания. При звуковых колебаниях воздуха в каждой точке среды происходят периодические чередования сжатия и разрежения, которые в любой точке среды создают то большее, то меньшее давление по сравнению с тем, какое было до начала звукового колебания, то есть когда среда (воздух) была в спокойном состоянии. Это избыточное (или недостаточное) давление и называют звуковым. За единицу давления, в том числе и звукового, принят паскаль (Па), который показывает давление силой в 1 ньютон (Н), равномерно распределенное по поверхности площадью в 1 квадратный метр (1 Па = Н/м²).
Звуковое давление по сравнению с нормальным атмосферным давлением составляет совсем небольшую величину. Например, громкий разговор в комнате будет развивать звуковое давление в миллион раз меньше атмосферного. Так почему же при столь незначительном давлении мы слышим звук? Вспомните, что звуковое давление получается путем сжатия и разрежения воздуха. Следовательно, наше ухо реагирует не на абсолютное давление, а именно на избыточное или недостаточное, то есть на изменения давления. Чтобы подтвердить это, сошлемся на такой пример. При спуске со второго этажа на первый постоянно действующее на наш организм атмосферное давление изменяется всего на 0,2 своей величины, и, естественно, ухо его не замечает. Но аналогичное по величине звуковое давление, действующее на барабанную перепонку уха (а именно такое звуковое давление развивает шум от работы реактивного двигателя самолета на расстоянии в несколько метров), способно вызвать болевые ощущения.
А какой же интервал звуковых давлений способно различать наше ухо? Разберемся по порядку.
Синусоидально изменяющееся во времени звуковое давление будет воздействовать на ухо и восприниматься нами как звук в том случае, когда оно не слишком мало и не слишком велико, а частота его не слишком мала и не слишком велика. Сколько ограничений сразу! Как же их понимать?
С постепенным уменьшением звукового давления слышимый нами звук будет становиться все тише и тише, пока наконец не перестанет быть слышимым. Это звуковое давление (или соответствующее ему значение силы звука) принято называть порогом слышимости. Для тона частоты 1000 Гц порогу слышимости соответствует звуковое давление в 2 х 10-5 Па или примерно двум десятимиллионным долям грамма. Столь малое давление вряд ли отметят лучшие микровесы.
Если теперь не уменьшать, а наоборот, постепенно увеличивать звуковое давление, то при некотором его значении мы уже не сможем различать звук, ибо появятся болевые ощущения. Эта вторая точка восприятия звука называется порогом болевого ощущения, а соответствующее ему звуковое давление будет в несколько миллионов раз больше звукового давления, соответствующего порогу слышимости. Между этими крайними точками и лежит та область звуковых давлений, которые воспринимает человек с нормальным слухом. А чтобы представить себе, как велика эта область, давайте продолжим аналогию с весами. Так вот, звуковое давление порога слышимости так относится к звуковому давлению порога болевого ощущения, как вес мухи относится к весу слона. Найдутся ли в мире такие весы, с помощью которых можно было бы определить вес мухи и вес слона? Думаем, что вряд ли. А слух нормального человека способен различать такие давления.
А чтобы нагляднее представить себе, сколь незначительна величина такого звукового давления, добавим, что при таком звуковом давлении амплитуда смещения частиц воздуха едва достигает десятой доли радиуса молекулы. И, естественно, услышать такой звук может только человек с нормальным слухом и в полной тишине.
Теперь о частоте звука. Что означает выражение: «не слишком мала и не слишком велика»? Ученые на ряде опытов установили способность человека воспринимать «на слух» звуковые колебания с частотами примерно от 30 до 16000 Гц. Почему примерно? Во-первых, потому, что этот участок частот (специалисты такой участок называют диапазоном) не постоянен и изменяется с возрастом. Установлено, например, что дети слышат звуки с частотой вплоть до 20000 Гц, а люди пожилого возраста только до 12 000 - 14 000 Гц. Во-вторых, это объясняется строением человеческого уха. Но об этом мы расскажем чуть позже.
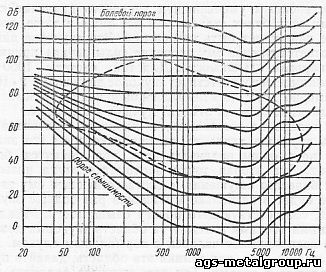
Рис. 5. «Семейство» равнослышимых кривых, называемых «кривыми равной громкости», показывает, как изменяется субъективное восприятие громкости звука в зависимости от высоты его тона.
Анализируя способность человека воспринимать различные по частоте звуки, ученые установили интересную особенность: чувствительность слуха к различным частотам не одинакова. Наибольшая чувствительность слуха лежит в диапазоне частот от 2500 до 4000 Гц и в обе стороны от него постепенно уменьшается. Кроме этого, при тихих звуках зависимость чувствительности уха от частоты звуковых колебаний больше, чем при громких звуках. На основе этих исследований были составлены так называемые кривые равной громкости, показанные на рисунке. Рассматривая этот график, вы, наверное, обратили внимание на не встречавшуюся ранее единицу исчисления, отложенную по вертикальной оси и обозначенную буквами дБ. Это безразмерная логарифмическая единица, называемая бел (Б). Однако бел довольно большая единица, и в практической деятельности обычно пользуются ее десятой частью, называемой децибел (дБ). Децибел показывает отношение каких-либо одноименных физических величин. Посмотрев еще внимательнее на этот график, вы, несомненно, обнаружите, что и частоты на горизонтальной оси тоже отложены в логарифмическом масштабе. Случайно ли это? Оказывается, нет. И дело здесь в субъективной оценке громкости, которая возрастает приблизительно пропорционально логарифму звукового давления. Но это не единственная причина. Оказывается, ощущение высоты тона, то есть частоты звука, также подчиняется логарифмическому закону, и значительно более точно, чем субъективная оценка громкости звука. Поэтому любое увеличение частоты звука в два раза всегда создает слуховое ощущение повышения тона на одну октаву, независимо от того, каким по частоте был первоначальный тон. К этому следует добавить, что в физике, да и в технике, часто прибегают к логарифмическому масштабу в том случае, когда на одном графике нужно показать величины, имеющие между собой очень большую разницу. А ведь разница в звуковых давлениях между порогом слышимости и порогом болевого ощущения очень велика. Если величину звукового давления, соответствующую порогу слышимости, выразить отрезком в один миллиметр, то величина звукового давления, соответствующая порогу болевого ощущения, выразится дорогой в несколько километров. Такой график начертить невозможно. Это позволяет сделать только логарифмический масштаб, так как при возрастании какой-либо величины в 10, 100, 1000 и т. д. раз ее логарифм увеличивается на 1, на 2, на 3 и т. д.
Несколько слов о самих звуках. Звуки с малой частотой называют низкими, а звуки с большой частотой - высокими. Низкие частоты, лежащие за порогом слышимости (до 20 Гц), называют инфранизкими или инфразвуковыми, а высокие частоты, также лежащие за порогом слышимости (выше 20 000 Гц), называют ультравысокими или ультразвуковыми. Наука акустика изучает как слышимые звуки, так и инфранизкие и ультравысокие. Ученые открыли, например, что рыбы «разговаривают» между собой инфранизкими частотами. Летучие мыши, наоборот, используют ультравысокие звуковые частоты. Исследуя образ жизни и повадки летучих мышей, ученые установили очень много интересного и полезного. Оказывается, например, чтобы летучая мышь могла летать ночью, в полной темноте, природа снабдила ее совершенным ультразвуковым эхолокатором, работающим следующим образом. При полете летучая мышь посылает в пространство короткие импульсы с частотой 25 000 - 50 000 Гц и длительностью 10 - 15 тысячных долей секунды, которые, попадая на препятствие, отражаются от него и возвращаются обратно. Слуховые органы летучей мыши способны воспринять отраженный сигнал даже в том случае, если он будет в 2000 раз слабее посланного. Более того, летучая мышь обладает способностью отличать свой отраженный сигнал среди постороннего шума, даже если этот шум в тысячи раз превосходит по силе эхо посланного ею сигнала. А расстояние до препятствия летучая мышь определяет (разумеется, инстинктивно) по времени, которое проходит с момента посылки сигнала до его возвращения.
Ультразвуковые колебания вообще очень широко используются в науке и технике, и о них можно было бы рассказать много интересного. Но мы немного отвлеклись от темы нашего разговора и сделали это только для того, чтобы показать, какое огромное значение имеют звуковые колебания и нашей жизни и окружающей нас природе.
Продолжим наш разговор о звуковых колебаниях. Вы, конечно, знаете, да и мы об этом говорили выше, что звуковые колебания распространяются не мгновенно, а постепенно, то есть объемы воздуха приходят в движение по очереди, как бы подхватываются волной, идущей от источника звука. Если в этом движении выделить одну колеблющуюся частицу, и проследить за ее поведением, и сравнить с другими частицами, лежащими на линии распространения звукового колебания, то мы заметим, как соседняя частица придет в колебательное движение несколько позже первой. Следующая частица придет в колебательное движение еще позже. Это запаздывание будет постепенно нарастать, пока мы не обнаружим частицу, колеблющуюся в такт с первой частицей. Оказывается, эта частица отстала от первой на целый период. Такие две частицы можно сравнить с бегунами на стадионе, когда один из них отстал от лидера на целый круг и одновременно с ним проходит линию финиша. Расстояние между двумя колеблющимися в такт частицами называют длиной волны данного колебания и обозначают греческой буквой л (лямбда). Численно длину волны можно выразить формулой: л = V x Т = V/f, где V - скорость распространения звука в данной среде (для воздуха эта скорость равна 330 м/с), Т - период колебания и f - частота.
Графическое изображение волнового процесса очень похоже на изображение развертки колебательного процесса, показанное на рис. 4. И в том и в другом случае графики представляют собой синусоиду. Но между ними есть и существенное отличие. Если при развертке колебательного движения мы по горизонтальной оси откладывали промежутки времени, то при изображении волнового процесса по той же оси мы откладываем расстояние (путь). Зная частоту звука и скорость его распространения в данной среде, можно легко определить длину его волны. Это нам очень понадобится при рассказе о некоторых особенностях магнитной записи звука.
Теперь несколько слов о строении нашего органа слуха и принципе его работы. Ухо человека принято делить на три части: наружное, среднее и внутреннее ухо. Наружное ухо состоит из ушной раковины, улавливающей поток звуков, и наружного слухового канала, по которому звуковая волна направляется к внутренним частям уха. В состав среднего уха входят барабанная полость и слуховые косточки, получившие названия: молоточек, наковальня и стремя. Наружное ухо отделено от среднего барабанной перепонкой. В состав внутреннего уха входит улитка, соединенная со слуховыми косточками. Именно они и относятся к органу слуха. Улитка имеет форму спирали и образует 2,5 завитка. Внутри улитки, заполненной особой жидкостью, есть несколько мембран, способных колебаться. На основной мембране расположен так называемый кортиев орган, слуховые клетки которого (а их бывает от 16 до 24 тысяч) имеют волоски, похожие на струны. К слуховым клеткам подходят чувствительные окончания нервных волокон слухового нерва, соединяющего ухо с височной долей больших полушарий головного мозга.
Звуковые колебания воздействуют на барабанную перепонку. Та, в свою очередь, передает эти колебания через слуховые косточки мембранам улитки, которые заставляют колебаться волоски кортиева органа. Именно здесь под воздействием колебаний жидкости внутреннего уха и происходит преобразование механических раздражений слуховых клеток в нервные импульсы, которые осознаются нами как смысловое сочетание звуков.
Хотя «механизм» работы нашего уха изучен довольно детально, некоторые вопросы до сих пор еще остаются загадкой для ученых. Действительно, как может нормальный человек слышать звуки с частотой от 30 до 16000 Гц? Если принять скорость звука в воздухе равной 330 метрам в секунду, то длина волны самого низкого звука будет равна 11 метрам и самого высокого звука - 2 сантиметрам, а улитка внутреннего уха представляет собой канал длиной всего в несколько сантиметров. Или, например, такой вопрос. Ученые установили, что на разные по частоте звуковые колебания реагирует та или иная часть улитки„а на воздействие отвечает сразу большое число слуховых клеток. Несмотря на это, человек (особенно в детском возрасте) способен различать ничтожное изменение звука по частоте. Ученые пытались создать механическую модель уха, которая могла бы столь же хорошо различать звуки по частоте, но их попытки пока не увенчались успехом. Может быть, в дальнейшем и удастся сконструировать кибернетическое ухо, которое поможет решить эти загадки. А пока мы можем только констатировать, что решающую роль здесь играет анализ раздражений в нашем мозгу.
